Partie 1/3 : Ordres de grandeurs selon l’AR5
par J.C. Maurin, Professeur agrégé de physique
On désigne par cryosphère l’ensemble des glaces terrestres. Son évolution, lors des dernières décennies, est souvent présentée comme préoccupante: il en résulterait une forte hausse des niveaux marins et un changement d’albédo et donc du bilan énergétique de la Terre. Cette première partie de l’article présentera quelques ordres de grandeurs pour les glaces terrestres.
On utilisera principalement les données du chapitre 4 du rapport AR5 WG1 (5th Assessment Report, Working Group 1) qui a été publié en 2013 par l’organisme intergouvernemental GIEC.
1. Ordres de grandeurs des volumes glaciaires
Le chapitre 4 [1] de l’AR5 indique quelques ordres de grandeurs pour l’ensemble des glaces terrestres (Figure 1 et original du tableau ici).
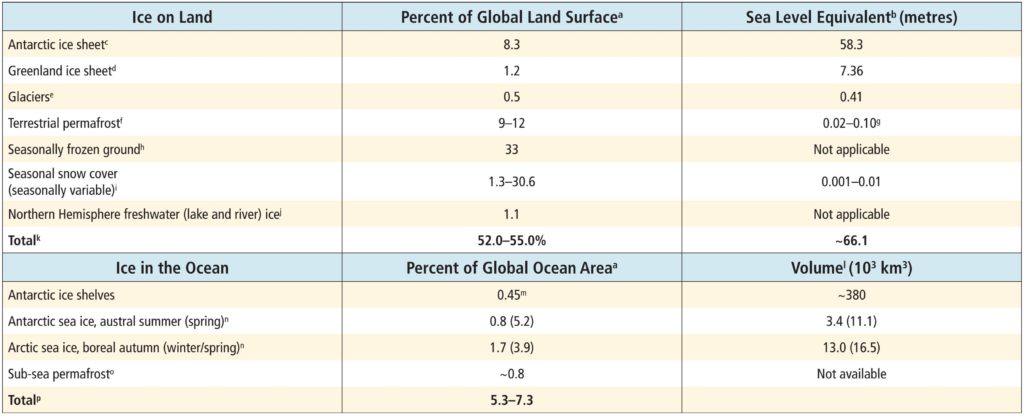
Antarctique [2] et Groenland (Ice Sheet ou calotte glaciaire) sont donnés en équivalent de hauteur d’eau sur l’océan (Sea Level Equivalent soit SLE = 58,3 m et SLE = 7,36 m) alors que les banquises (Sea Ice ou glace de mer) sont données directement en volume, ce qui ne facilite pas les comparaisons.
La légende du tableau 4.1 (ice density = 917 kg m–3, seawater density = 1028 kg m–3, océan area = 362,5 Mkm²) permet d’élaborer un tableau plus lisible (Figure 2a) et de tracer ensuite un graphe de type secteur ou camembert (Figure 2b).
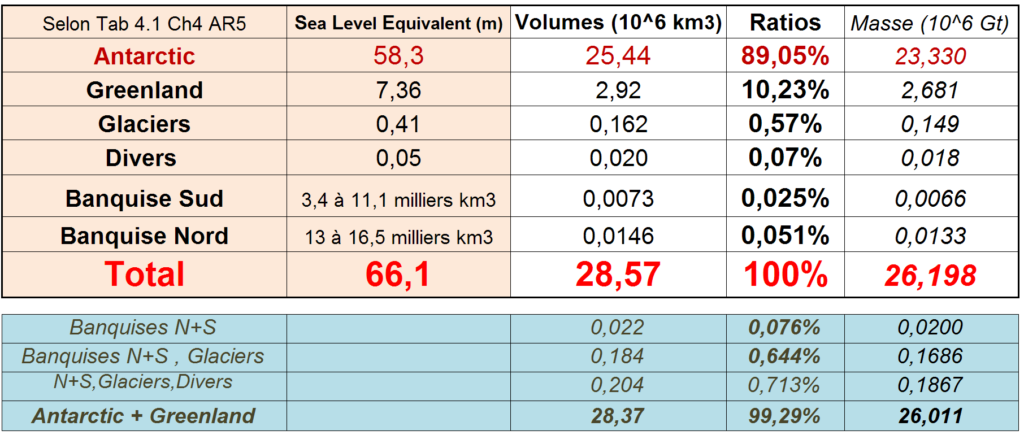
La surface océanique variant en cas de hausse des niveaux marins, le calcul du volume pour ‘Antarctic’ et ‘Greenland’ utilise les facteurs de conversion (SLE→ volume) de l’AR4.
Les glaces de mer (banquises ou sea ice) présentent une variation annuelle : on a donc reporté la moyenne. Permafrost, Snow, et Lake & River Ice sont regroupés dans la rubrique « Divers ». Le tableau sur fond bleu permet des comparaisons supplémentaires. 1Gt = 1 gigatonne = 1012 kg, 1 km3 = 109 m3
SCE publie chaque mois l’évolution de l’étendue de la banquise Nord : notons que le volume de glace en Antarctique représente 25,44/ 0,0146 ≈ 1750 fois le volume moyen de la banquise Nord.
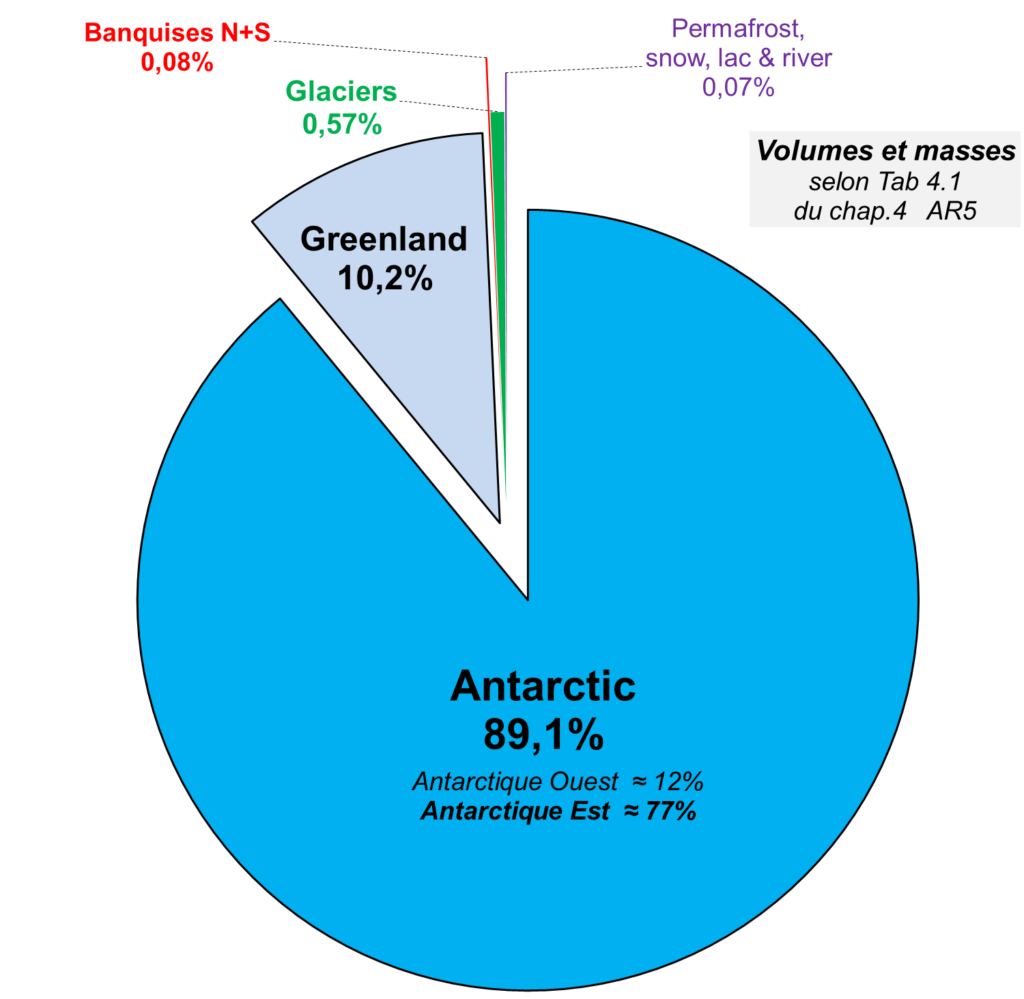
Selon l’AR5, la masse totale de la cryosphère serait ≈ 26,2 1018 kg , et son volume ≈ 28,6 1015 m3. La somme (banquises + glaciers + permafrost, snow, lac & river) correspond à 0,204 106 km3 soit 0,7% de la cryosphère. Le volume de glace en Antarctique (89,1% de la cryosphère) est donc 125 fois plus grand.
Le volume de glace en Antarctique, de loin le premier contributeur au volume de la cryosphère, ne semble pas être connu très précisément : en effet, dans le précédent rapport AR4 [1] du GIEC, la Table 4.1 en page 342 donnait pour ice sheet Antarctica SLE ≈ 56,6 m alors que l’AR5 [1] donne désormais SLE ≈ 58,3 m (Figure 1). La figure 3 illustre l’ampleur de cette correction sur l’Antarctique, à 6 ans de distance, entre AR4 et AR5.
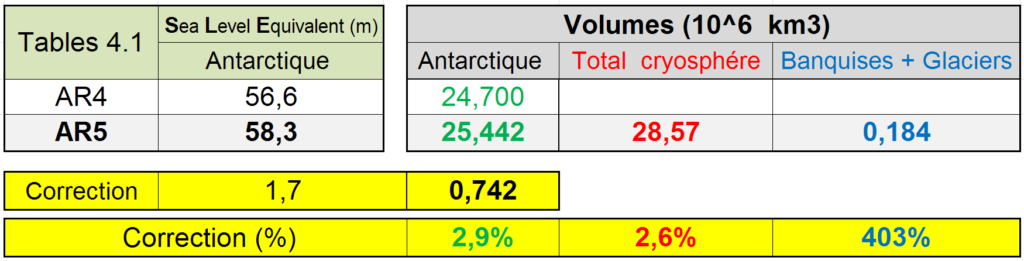
La différence 58,3 – 56,6 = 1,7 m correspond à une correction de 2,9% sur l’Antarctique ou bien à un volume de 0,742 millions de km3. La correction du volume de glace en Antarctique entre AR4 et AR5 est 4,03 fois plus grande que la somme des volumes (Banquises + Glaciers).
2. La principale composante de la cryosphère : l’Antarctique
Le continent Antarctique est découvert vers 1820. Dumont d’Urville y débarque en 1840, il y a donc seulement 180 ans. On distingue deux parties dans l’Antarctique suivant que l’on se trouve à l’Est ou à l’Ouest de la chaîne Transantarctique. Le seul Antarctique Est contiendrait plus de 85% des glaces de l’Antarctique soit plus de 75% de la cryosphère (ici).
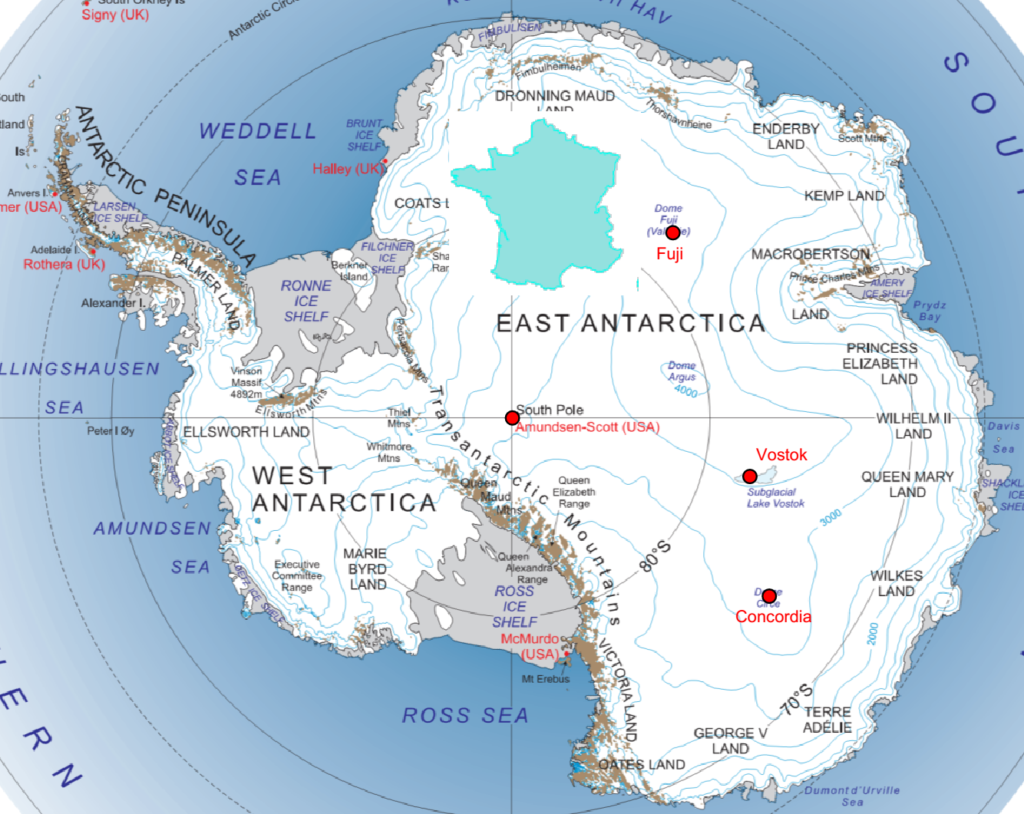
- Les observations sont donc assez récentes en Antarctique Est (≈ 77% de la cryosphère), et les rares observatoires sont répartis sur une surface bien plus grande que l’Europe. Les estimations récentes des volumes glaciaires, en Antarctique et au Groenland, sont surtout basées sur des observations aériennes (altimétrie et gravimétrie), complétées par des modélisations;
- Le chapitre 4 de l’AR5 (page 352, Fig. 4.16) indique une perte de masse glaciaire de -2050 Gt (1Gt = 1 gigatonne = 1012 kg) dans le bilan gain/perte (1992-2012) en Antarctique (cette perte de masse représente 0,009% de la masse de glace en Antarctique).
Mais, a contrario, certains articles [2] postérieurs à l’AR5, donnent un gain dans le bilan gain/perte 1992-2012. Le manque de recul, sur les techniques de gravimétrie ou d’altimétrie, sur la modélisation, ainsi que la rareté des observations in situ, doivent inciter à une certaine prudence sur le bilan gain/perte, surtout en Antarctique Est (≈ 77% de la cryosphère).
La deuxième composante, le Groenland (10,2% de la cryosphère), est mieux connue que l’Antarctique. L’AR5 indique une perte de masse glaciaire de -2985 Gt (1992-2012), ce qui correspond à -0,1% de la masse de glace du Groenland.
3. Ordres de grandeurs en énergie [3]
3.1 Albédo
La puissance moyenne atteignant la haute atmosphère de la Terre, en provenance du Soleil, est estimée à ≈ 176 1015 W. Environ 123 1015 W finiront par être réémis en infrarouge vers l’espace et environ 53 1015 W seront renvoyés sous forme visible (albédo = 53/176 ≈ 0,3).
Selon l’AR5 (Fig 2.11 en page 181 ici), les nuages et l’atmosphère seraient responsables d’environ 76% des 53 1015 W renvoyés en visible.
Sur les 24% restants, moins de la moitié est imputable à la cryosphère : les surfaces englacées interviennent dans l’albédo mais jouent actuellement un rôle secondaire. Parmi les composantes de la cryosphère, les zones proches du pôle Sud sont prépondérantes pour les surfaces englacées (Figure 5).
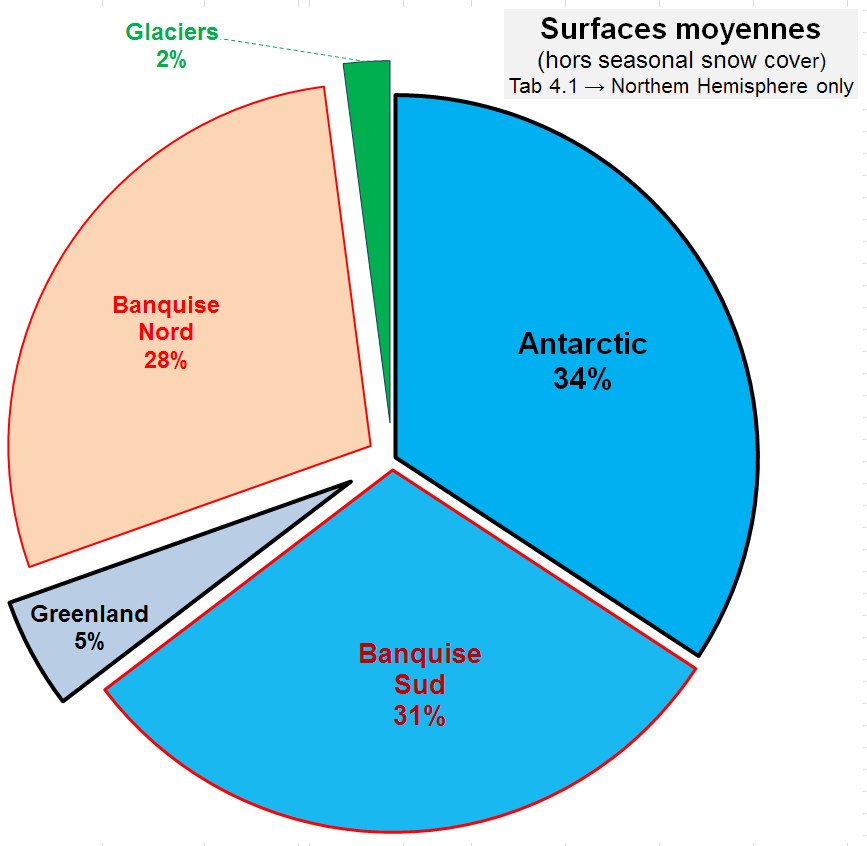
des composantes de la cryosphère [1] [3]
Les surfaces proches du pôle Sud, à savoir Antarctic (ice sheet + ice shelves + sea ice), correspondent en moyenne à ≈ 25 106 km². Les surfaces Greenland + Glaciers + Arctic sea ice correspondent en moyenne à ≈ 12,5 106 km², soit ≈ 2 fois moins. La couverture neigeuse est omise car le tableau 4.1 de l’AR5 donne seulement l’hémisphère Nord (en moyenne annuelle, l’étendue ≈ 15,8 106 km²). Voir également cet article de SCE). La surface totale correspondant au graphe en secteur est ≈ 37,5 10 6 km² soit 7,3% de la surface terrestre ≈ 510 106 km².
3.2 Fonte de la cryosphère
La fonte complète des glaces terrestres (≈ 28,6 1015 m3 soit 26,2 1018 kg) nécessite une énergie E = E1+E2.
Avec 333,5 kJ pour la fonte de 1 kg de glace à 0°C, on obtient l’estimation E1 ≈ 8,75 1024 joules.
On doit également ajouter l’énergie E2 nécessaire pour réchauffer la glace jusqu’à sa température de fonte.
(E2 ≈ 1,05 1024 joules pour réchauffer 28,6 1015 m3 de glace depuis -20°C vers 0°C) [3].
L’ordre de grandeur pour la fonte complète de la cryosphère est donc E1+E2 ≈ 9800 1021 joules soit E = 9800 ZJ.
Cette énergie E est considérable comme le montrent les comparaisons suivantes :
- Les différentes sources d’énergie fournissent annuellement à l’humanité Eh ≈ 0,6 ZJ.
L’énergie E pour fondre l’ensemble des glaces correspond donc à 9800/0,6 = 16 000 années de consommation. - Les théories « effet de serre » ou « échanges radiatifs » permettraient le calcul d’un « forçage radiatif ».
Le chapitre 8 de l’AR5 (Fig 8.15 AR5 p.697) chiffre la part anthropique de ce « forçage radiatif » entre 1 et 3,5 W/m².
En prenant 2,3 W/m², sur la surface terrestre, pour une durée d’un an, on obtient l’énergie Efr = 37 10 21 J.
Le ratio avec l’énergie de fonte E est 9800/37 ≈ 265 (2 à 3 siècles seraient donc au minimum nécessaires).
En réalité, la grande majorité de l’énergie Efr serait absorbée par l’océan et la durée serait bien plus longue.
Cette durée pourrait même être infinie (si Efr ≈ 0) car les notions « effet de serre » ou « forçage radiatif », mises en œuvre dans les programmes de modélisation climatique, ne sont pas admises par l’ensemble des physiciens : voir cet article sur SCE ou bien celui-ci.
4. Conclusions
- La cryosphère c’est en premier lieu les zones proches du pôle Sud : banquises et glaciers ne représentent ensemble que 0,7% du volume de la cryosphère alors que la seule partie Est de l’Antarctique, bien moins connue, représente plus de 75% de la cryosphère, soit 107 fois plus.
- La simple correction du volume de glace en Antarctique, entre les rapports du GIEC AR4 (2007) et AR5 (2013), est 4 fois plus grande que le volume (Banquises + Glaciers).
- Les variations actuelles de la cryosphère restent négligeables si on les compare à celles du passé : l’ensemble des glaces terrestres, il y a 20 millénaires, devait avoir un volume au moins double du volume actuel. En effet, la fonte des glaces (entre -18 ka et -8 ka) fait monter le niveau des océans de ≈ 120 m contre 66 m SLE (Sea Level Equivalent à la Figure 1).
La deuxième partie de l’article (2/3) commentera les choix rédactionnels du GIEC pour le chapitre 4 de l’AR5 et donnera des ordres de grandeurs complémentaires pour les banquises et les glaciers.
NOTES
[1] Rapports du GIEC
Ch.4 AR5 (2013) https://www.ipcc.ch/site/assets/uploads/2018/02/WG1AR5_Chapter04_FINAL.pdf
Ch.8 AR5 (2013) https://archive.ipcc.ch/pdf/assessment-report/ar5/wg1/WG1AR5_Chapter08_FINAL.pdf
Ch.4 AR4 (2007) https://www.ipcc.ch/site/assets/uploads/2018/02/ar4-wg1-chapter4-1.pdf
Spécial Report Océan and Cryosphère (2019) https://www.ipcc.ch/srocc/
[2] Antarctique Les observatoires en Antarctique https://fr.wikipedia.org/wiki/Liste_de_bases_antarctiques
Refroidissement en Antarctique: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1002/2017JD027435
Neige en Antarctique: https://www.nature.com/articles/s41558-018-0356-x
Les gains à l’Est sont inférieurs aux pertes à l’Ouest :
Constraining the mass balance of East Antarctica https://agupubs.onlinelibrary.wiley.com/doi/full/10.1002/2017GL072937
Bamber et al (2018) https://iopscience.iop.org/article/10.1088/1748-9326/aac2f0/meta
Les gains à l’Est sont supérieurs aux pertes à l’Ouest :
‘Mass gains of the Antarctic ice sheet exceed losses’ Zwally et al (2015) doi:10.3189/2015JoG15J071 https://pdfs.semanticscholar.org/7cca/82fa14de7865472b781289636c1f172c459f.pdf
[3] Le tableur « Cryosphère 1 » met en forme les données dans 4 feuilles de calcul.
Il y a une petite coquille : 0,0146/25,44 ≈ 1750
@ Climarco
Merci beaucoup pour votre lecture attentive, la coquille est corrigée.
Très intéressant et instructif. Merci!
Pour ma gouverne, 1 km3 vaut 1E9 m3 ou 1E3 m3?
Bien à vous
Pierre
Merci pour votre lecture.
On trouve un milliard de m3 dans un km3, donc 1E9
Merci bcp pour cette clarification.
1 km3 pourrait aussi vouloir dire 1 millier de m3
Vu deux ans après : JC Maurin vous dit un km3 fait 10^9m3.
Càd 1000 m3 x 1000m3 x 1000m3. Un cube de 1km de côté.
Il est vrai qu’à l’école on raisonnait plutôt sur des cm3, dm3 et des m3. Mais il y a la même proportion entre le mm3 et le m3. Puisque une bande de 1000mm fait une barre de 1000mm3, en longueur, largeur et hauteur, soit 1000x1000x1000, ce qui donne 10^9 mm3 dans un m3.
La confusion vient sans doute des litres, qui valent 1 dm3 ; il y a donc 10x10x10= 1000 litres ou dm3 dans un m3.
On pourrait continuer avec les cl et les ml!
Non. 1 km3 = 1 milliard de m3