Carbone 14 et effet Bombe

par J.C. Maurin, Professeur agrégé de Physique

Les essais thermonucléaires (1952-1963) ont constitué une expérience d’ajout brutal de carbone 14 dans l’atmosphère. Le présent article utilise les observations de cet « effet bombe » pour estimer la durée de séjour du ¹⁴CO₂  et la taille des réservoirs avec lesquels l’atmosphère échange depuis 60 ans. Ces estimations sont en contradiction avec une croissance exclusivement anthropique du CO₂ dans l’atmosphère.

Partie 1/3 de l’article (Carbone 14 et effet Suess)

1. Le carbone 14 dans l’atmosphère [1]

Le carbone existe habituellement sous 3 formes isotopiques : ¹²C ,¹³C et ¹⁴C à l’état de traces.

Figure 1a. [5] La différence entre CO₂ anthropique et CO₂ atmosphérique se trouve dans les proportions du mélange des isotopes : le CO₂ anthropique est appauvri en ¹³C et ¹⁴C.

La probabilité de désintégration du ¹⁴C est constante, en conséquence le ¹⁴C subsistant au temps t va suivre une loi de décroissance exponentielle.

Figure 1b. [5] Quelques ordres de grandeurs pour la désintégration du carbone 14.

Figure 1c.  [5] On évalue le ¹⁴C en mesurant l’écart relativement à une référence étalon. La mesure est corrigée pour obtenir une grandeur normalisée Δ¹⁴C.

On a Δ¹⁴C = 0‰  pour l’équilibre dynamique initial → production en haute atmosphère = disparition par désintégration. De nombreuses observations aboutissent à la reconstitution du carbone 14 dans l’atmosphère de la Figure 1d.

 

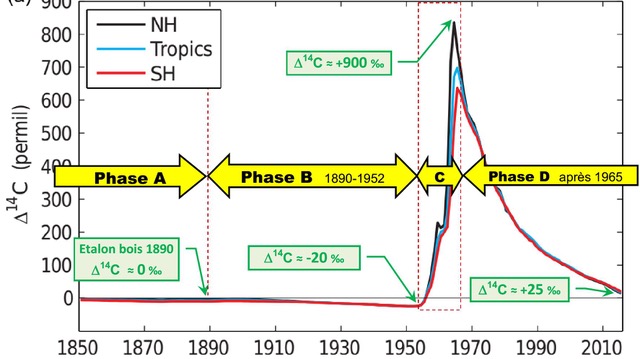
 Figure 1d. Reconstitution du Δ¹⁴C pour le CO₂ atmosphérique depuis 1850 (ici fig1). NH et SH correspondent aux hémisphères Nord et Sud.

2. Interprétation des évolutions du carbone 14 (Fig.1d)

Phase A. La production de ¹⁴C par les neutrons cosmiques équilibre la désintégration du stock total de ¹⁴C  → Δ¹⁴C  = 0 ‰

Phase B. L’atmosphère s’appauvrit en ¹⁴C : on passe de  Δ¹⁴C  = 0 ‰ en 1890 vers ≈ -20 ‰ en 1952 (effet Suess).

Phase C. On constate que Δ¹⁴C  passe de -20 ‰  vers + 900 ‰. Le tableau Fig. 2 indique que l’atmosphère en 1963 comporte presque 2 fois plus de molécules ¹⁴CO₂ que l’atmosphère en 1952.

L’explosion d’une bombe H produit un flux de neutrons qui vont créer, à partir de l’azote atmosphérique, l’isotope ¹⁴C en grande quantité: ¹⁴N + n  → ¹⁴C + 1p. Dans l’atmosphère,¹⁴C s’oxyde rapidement en ¹⁴CO₂.

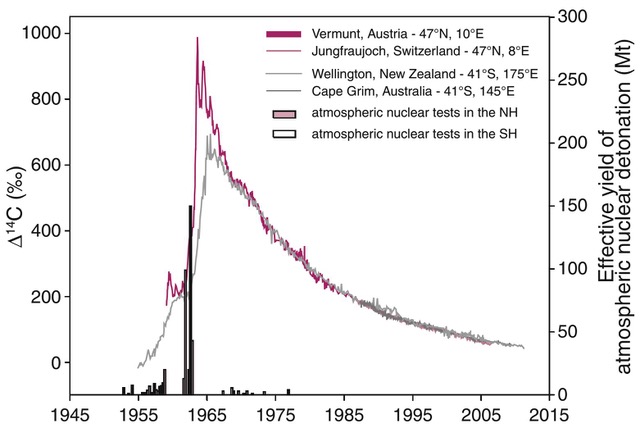
 Figure 2. Les phases C et D  (ici fig 4.6) [2] Essais thermonucléaires 52-63 puis décroissance de Δ¹⁴C suivant plusieurs observatoires. Les barres noires verticales représentent les essais thermonucléaires (UNCEAR). A l’exception de quelques essais vers 1967-1980 (France/Chine/U.K.), les essais thermonucléaires dans l’atmosphère se produisent presque totalement entre 1952 et 1963 dans l’hémisphère Nord. L’ajout de ¹⁴C date principalement des années 1961 -1963.

Phase D (Fig. 1d et 2).  A la fin 1965, ¹⁴CO₂ s’est presque réparti également dans les 2 hémisphères, le nombre de molécules ¹⁴CO2  dans l’atmosphère décroît ensuite très rapidement.

Les causes de cette décroissance sont multiples et sont discutées ci-après :

• Le tableau Fig.1b indique que la décroissance radioactive est presque négligeable : en 50 ans, il disparaît seulement 0.6 % du ¹⁴C issu des essais thermonucléaires mais les observations du Δ¹⁴C (Fig. 2) montrent une décroissance bien plus rapide.
• L’explication principale se trouve dans les échanges de CO₂ entre l’atmosphère et d’autres réservoirs. Biosphère, océan, et autres absorbent le CO₂ atmosphérique chargé en ¹⁴CO₂ (les sorties) mais envoient dans l’atmosphère (les entrées) un CO₂ initialement proche de l’ancien équilibre, donc peu chargé en ¹⁴CO₂. Progressivement, le carbone 14 des essais nucléaires se repartira entre les différents réservoirs : atmosphère, océan, biosphère, etc. Les entrées et sorties finiront par échanger le ¹⁴CO₂ de façon presque égale : on atteint un équilibre provisoire (≈ 50ans selon Fig.5b).
• Ensuite, la lente désintégration radioactive éliminera la totalité du ¹⁴C des essais atomiques. Cette élimination sera presque complète en quelques dizaines de millénaires selon le tableau Fig.1

3. Echanges entre réservoirs

Dans les échanges de CO₂ entre atmosphère et autres réservoirs, comment estimer la vitesse des échanges et la taille des réservoirs ?

Figure 3a. Schéma A : Échanges lents entre réservoirs de taille comparable. Un ajout instantané va dans un premier temps se répartir dans l’atmosphère en environ 2 ans selon la Figure 2. L’atmosphère échange ensuite avec d’autres réservoirs, la vitesse des échanges est symbolisée par les flèches bleues →  si les échanges sont lents alors la durée Ta est grande.

A long terme, l’asymptote nous renseigne sur la taille apparente des réservoirs : pour une asymptote ≈ 0,5 cela indique que l’on échange avec des réservoirs dont la taille apparente est comparable à celle de l’atmosphère. A long terme, l’atmosphère du schéma A contiendra 1/2 de l’ajout initial (0.5) tandis que les autres réservoirs contiendront l’autre moitié de l’ajout initial. On a 0.5/0.5 = 1, ainsi, une mesure sur l’asymptote permet d’estimer la taille apparente des autres réservoirs.

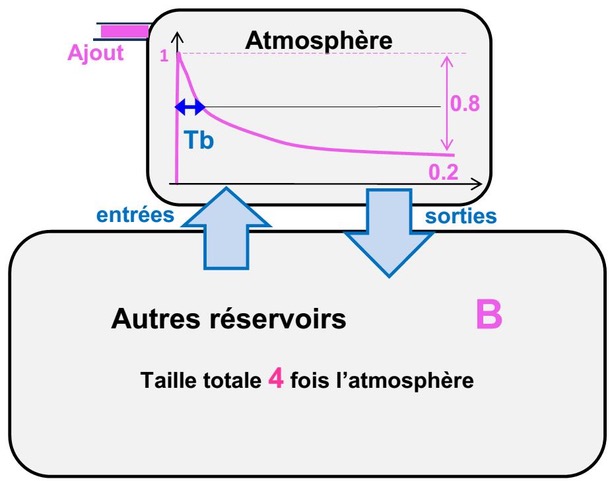
Figure 3b. Schéma B : Échanges rapides entre réservoirs de tailles différentes. La taille des flèches bleues symbolise ici une vitesse d’échange rapide et Tb est une durée plus courte que Ta. Pour avoir seulement 0.2 = 1/5 de l’ajout initial qui reste dans l’atmosphère, il est nécessaire que l’échange se fasse entre des réservoirs de tailles très différentes. Lorsque la répartition est presque terminée, l’asymptote indique que l’ajout est réparti entre réservoirs tels que 0,8/0,2 = 4. Les autres réservoirs ont donc une taille apparente 4 fois plus grande que l’atmosphère. A terme, la répartition de l’ajout initial est de 20 % dans l’atmosphère et 80 % dans les autres réservoirs.

 4. Durée de séjour pour ¹⁴CO₂

Pour caractériser la vitesse des échanges on peut utiliser la durée de séjour,
celle-ci est définie par le rapport  [CO₂] / sortie annuelle. Si les sorties annuelles représentaient par exemple 25% du taux de CO₂, alors l’atmosphère se renouvellerait en 4 ans (durée de séjour). A partir de l’effet Suess en 1950 (ici § 6) on a obtenu une durée de séjour comprise entre 7 et 13 ans pour le CO₂ anthropique. L’effet Bombe permet une autre estimation de la durée de séjour, mais pour ¹⁴CO₂

 

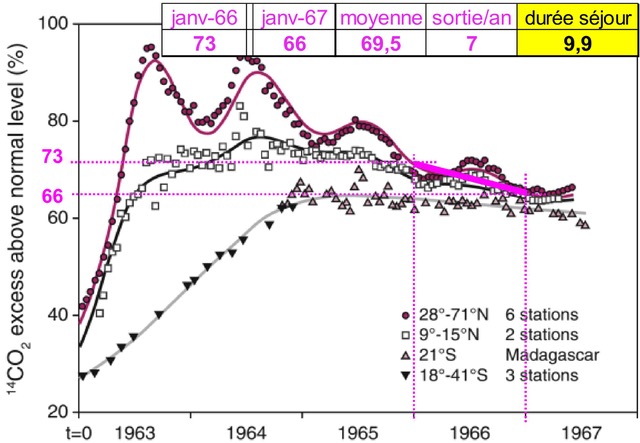
Figure 4. Estimation de la durée de séjour pour ¹⁴CO₂  [5] et Fig 4.8 ici. L’échelle verticale correspond à 10 x Δ¹⁴C, elle est donc en %. Les oscillations annuelles dans l’hémisphère Nord (en violet) indiquent probablement des échanges saisonniers avec la végétation. L’estimation [CO₂] / sortie annuelle  = 69.5 /7 = 9,9 ans est obtenue avec les mesures de 6 stations de l’hémisphère Nord en 1966.

Le choix de l’année 1966  permet d’avoir une estimation des sorties uniquement vers les autres réservoirs car :

– d’une part, la répartition entre hémisphères est presque terminée en 1966.

– d’autre part, 70% du carbone 14 est encore dans l’atmosphère et seulement 30% est passé dans les autres réservoirs: les entrées en 1966 sont encore très peu différentes de la période précédant les essais nucléaires.

On a donc une durée de séjour ≈ 10 ans pour le ¹⁴CO₂ (Fig.4). Pour d’autres estimations de la durée de séjour, voir ici en page 13).

5. Etude de la décroissance du Δ¹⁴C (phase D de la Figure 1d).

Pour pouvoir estimer la taille apparente des réservoirs, il faut au préalable estimer quel est le niveau d’équilibre en 2015. Celui-ci n’est pas resté stable depuis 1950 (Δ¹⁴C = -20 ‰) car, d’une part, l’homme injecte du CO2 anthropique (effet Suess), ce qui diminue Δ¹⁴C, d’autre part, l’industrie nucléaire et les quelques essais nucléaires des années 67-80 ont produit des neutrons donc du ¹⁴C, ce qui augmente Δ¹⁴C. Les 2 corrections ont donc des effets opposés.

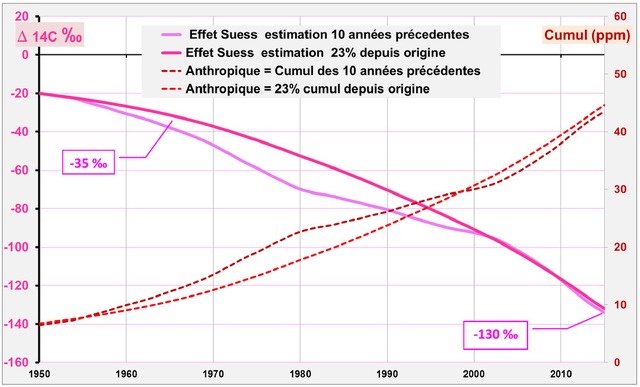
Figure 5a [5]  [2]. Une estimation de l’effet SUESS est réalisée à partir de l’effet SUESS de 1950, en corrigeant via le rapport des émissions anthropiques  entre 1950 et 2015. La correction peut aussi être calculée par comparaison des émissions anthropiques des 10 années précédentes soit (1940-1950) versus (2005-2015). Les 2 calculs donnent: Δ¹⁴C ≈ -130 ‰. en  2015  et Δ¹⁴C ≈ -35 ‰. en 1965. Cette correction est utilisée à la Fig. 5b.

On peut désormais estimer la taille apparente des réservoirs (cf. §3) qui échangent avec l’atmosphère depuis 1965.

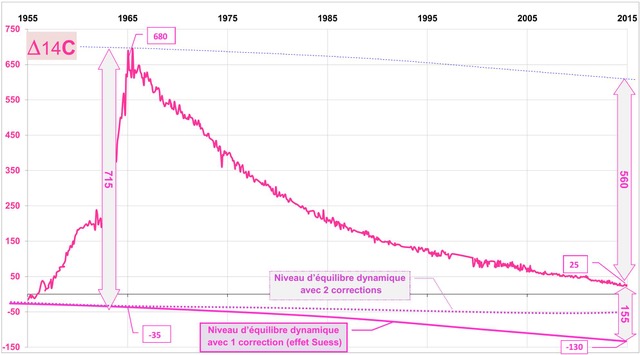
Figure 5b Evolution de  Δ¹⁴C [4] [5]. On utilise les données [4] de Wellington (Baring Head et Makara dans l’hémisphère Sud) afin que la répartition soit presque terminée entre hémisphères. Avec correction du seul effet Suess, le rapport 560/155= 3.6 indique que l’atmosphère échange le ¹⁴CO₂ avec des réservoirs ≈ 3.6 fois plus grands.

La proportion restant dans l’atmosphère est ≈ 155/715 = 22 % alors que 78% sont passés dans les autres réservoirs. La décroissance de Δ¹⁴C est donc proche du schéma B de la Fig. 3b.

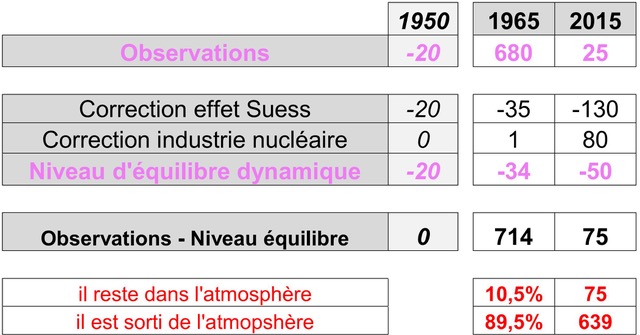
Figure 5c. Une seconde correction concerne l’industrie nucléaire, productrice de neutrons, qui  provoquent une genèse supplémentaire de carbone 14. Cette correction agit donc a contrario de l’effet Suess, et sa valeur, difficile à estimer, serait comparable. [2] P. Jean-Baptiste 2003. Le tableau donne un exemple de l’effet des 2 corrections simultanées : on arrive à une estimation des autres réservoirs ≈ 639/75  = 8.5 fois plus grands que l’atmosphère.

Le calcul de la Figure 5b est donc prudent : les autres réservoirs sont au moins 3.6 fois plus grands que l’atmosphère (max 22 % dans l’atmosphère et min 78 % dans les autres réservoirs), sans qu’il soit possible de faire un calcul précis.

Remarques : Les molécules ¹⁴CO₂ et ¹²CO₂  différent par leur masse mais le fractionnement isotopique est inférieur à 10%. La molécule  ¹⁴CO₂ n’est pas stable, mais la décroissance radioactive en 50 ans du carbone 14 n’est que de -0.6%. Sur 50 ans, les molécules doivent donc avoir des comportements proches, à défaut d’être identiques.

Les observations montrent qu’il faudrait utiliser des échanges avec des réservoirs au moins 3,6 fois plus grands que l’atmosphère. Les échanges sont rapides : il faudrait considérer un renouvellement du CO₂ atmosphérique en moins de 10 ans (Fig.4). La Figure 5d illustre la conséquence de ces estimations.

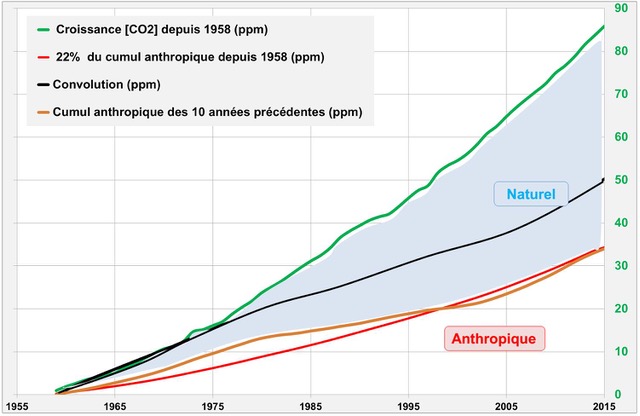
Figure 5d [5] [3]. L’augmentation de la taille des réservoirs entraînerait une proportion (Fig.5b) pour le CO₂ anthropique restant dans l’atmosphère ≈ 155 /715 ≈ 22%  (courbe rouge). Une deuxième estimation utilise la durée de séjour (Fig.4) : le CO₂ anthropique présent dans l’atmosphère correspondrait au cumul anthropique des 10 années précédentes (courbe marron). Une troisième estimation (courbe noire) correspond à la convolution des émissions anthropiques avec l’effet bombe de la Fig.5b (corrections Suess + industrie nucléaire).

Ces 3 estimations sont toutes inférieures à la croissance du CO₂ mesurée à Mauna Loa (courbe verte). Pour retrouver la totalité de la croissance du CO₂ mesurée à MLO, il est nécessaire de compléter par des apports nets non anthropiques, c’est-à-dire naturels (surface bleue). La croissance depuis 1958 (+86 ppm) serait alors mixte : en partie anthropique et en partie naturelle, sans qu’il soit possible de calculer exactement la répartition anthropique /naturelle.

La fin de l’article (à suivre) montrera que l’on peut directement comparer la courbe « effet Bombe » de la Fig.5b  avec une courbe analogue correspondant à la thèse du groupe intergouvernemental GIEC.

6. Références

1. Propriété du carbone 14 :    RadiocarbonDetermination     Fiche IRSN

2. Variabilité naturelle et anthropique pour ¹⁴C :

– H.E. Suess, « Radiocarbon Concentration in Modern Wood», Science, vol. 122, n^o3166,‎1955,  (DOI 10.1126/science.122.3166.415-a).
– Stuiver & Quay 1981  https://www.sciencedirect.com/science/article/pii/0012821X81900406?via%3Dihub
– Tans, De Jong & Mook1979   https://www.nature.com/articles/280826a0
– P. Jean-Baptiste, M. Paterne 2003 DOI: 10.105l/radiopro:2003017

3. Emissions anthropiques :  CDIAC.

– [CO₂] dans l’atmosphère  ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_annmean_mlo.txt
– [CO2] avant 1958   ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/law/law2006.txt

4. Données¹⁴CO₂  New Zealand : ftp://ftp.niwa.co.nz/tropac/co2/14co2/

Données ¹⁴CO₂  Austria :  https://cdiac.ess-dive.lbl.gov/trends/co2/cent-verm.html

Turnbull (2017) :  https://www.atmos-chem-phys.net/17/14771/2017/acp-17-14771-2017.pdf

5. La feuille de Calcul  « Carbone 14 effet bombe » met en forme les données d’observations.

Partie 1/3 de l’article (Carbone 14 et effet Suess)