par J.C. Maurin, Professeur agrégé de physique

A partir des notions intuitives de chaleur et température, les physiciens (Carnot, Thomson, Clausius, Maxwell, Boltzmann) arrivèrent progressivement à la notion scientifique de température thermodynamique. La Conférence Générale des Poids et Mesures  adopta en 1927 l’échelle thermodynamique proposée en 1911, puis l’unité kelvin en 1954.
La notion de température thermodynamique nécessite que l’équilibre thermique soit atteint, ce qui n’est pas le cas dans l’atmosphère de la Terre. Il n’existe pas une « température thermodynamique de l’atmosphère ». A défaut, on utilise une « moyenne des températures » mesurées en divers points de l’atmosphère. Mais la température thermodynamique étant une grandeur intensive, une moyenne, quelle que soit son élaboration, ne peut jouer qu’un rôle d’indicateur. L’usage est néanmoins d’utiliser le kelvin pour les indicateurs. On exprimera de préférence les variations des indicateurs sous forme relative. L’indicateur va être dépendant de l’échantillonnage (spatial et temporel) des mesures et surtout de son mode d’élaboration.

1. Les ordres de grandeurs

Capacité thermique océan et atmosphère

Le tableau ci-dessous donne les ordres de grandeurs des capacités  thermiques.

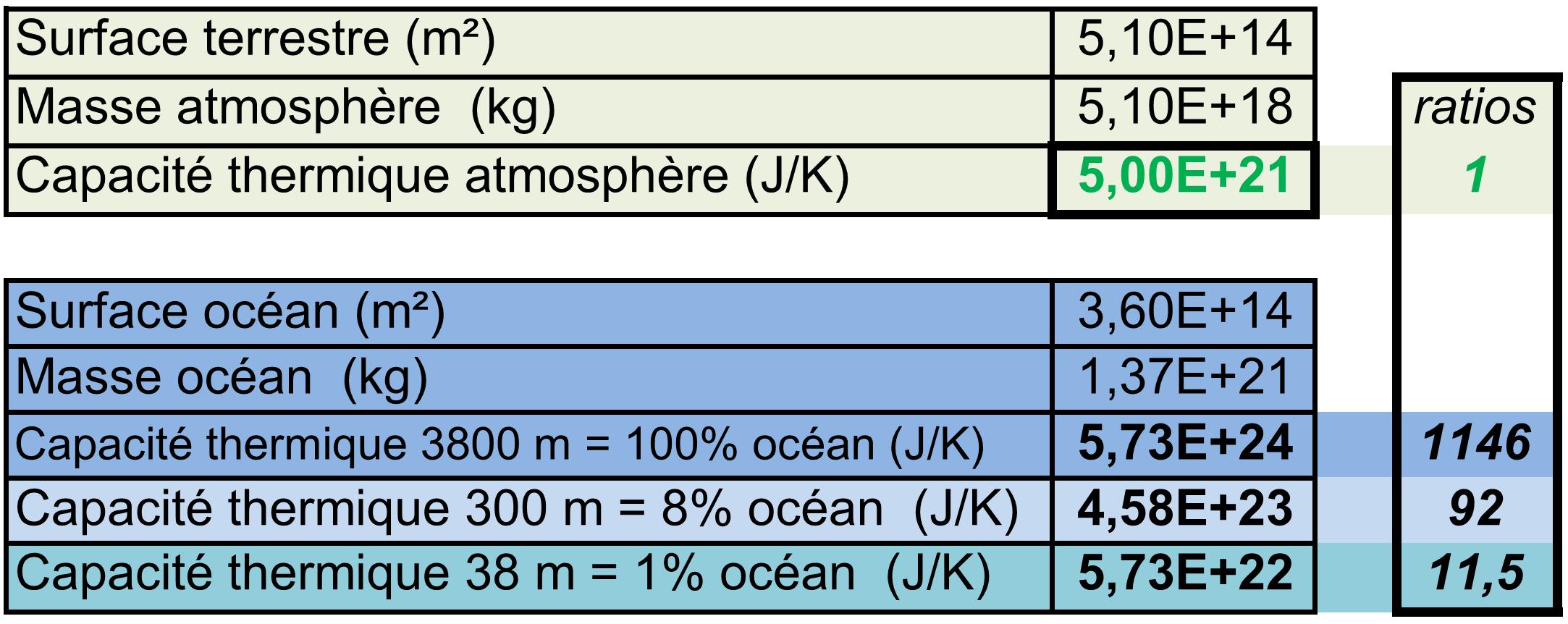Figure 1. [3]  Ordres de grandeurs. La profondeur moyenne de l’océan est ≈ 3800m.

Il faut fournir à l’atmosphère une énergie ≈ 5 10 ²¹J pour provoquer une hausse de 1 kelvin. Cette même énergie provoque une hausse de température pour l’océan de seulement 1/1146 = 0.00087 K, mais la durée nécessaire se chiffre en millénaires. Pour une durée de quelques décennies, l’océan ne peut être concerné dans les 3800 m de profondeur. Les seuls 38 premiers mètres d’océan ont une capacité thermique 11.5 fois plus grande que celle de la totalité de l’atmosphère. La forte capacité thermique de l’océan entraîne une plage de température réduite pour l’atmosphère proche de l’océan.

Incertitude sur la valeur moyenne

La valeur moyenne de la température pour la très basse atmosphère serait comprise entre 13°C (286 K) et 16 °C (289 K). La différence de puissance rayonnée entre 286 K et 289 K par un corps noir de même surface que la Terre est ≈ 8000 TW. Par comparaison, l’humanité consomme annuellement une énergie ≈ 0.5 10 ²¹ joules (ici) → puissance ≈ 16 TW soit 0.2% de 8000 TW.

Variabilité spatiale

Les températures mesurées par les stations météorologiques, au sol, donnent des valeurs comprises entre 55°C (328K) et -90°C (183K). Les températures présentent donc un écart maximal de 328-183 = 145 K (sur les continents et non sur l’océan). Le rapport entre la plage de variation et la moyenne est 145/286 = 0.507  ou 145/289 = 0.502  soit environ 50%. Pour le calcul des variations relatives, on utilisera comme valeur moyenne 287 K (au sol) et 265 K (à l’altitude de 3.5 km).

Variabilité temporelle

Dans un même lieu, les écarts de température au sol atteignent  20°C dans la journée et 50°C sur l’année. Soit une variabilité journalière de 20/287= 0.07 ou 7% et une variabilité annuelle de 50/287 = 0.17 ou 17%.

2. Les indicateurs UAH et RSS

C’est la température thermodynamique qui est utilisée dans les lois physiques régissant le rayonnement du corps noir. Dans le cas idéal du corps noir, on peut définir une température de rayonnement équivalente à la température thermodynamique.
Depuis 1979, des radiomètres, à vocation météorologique, embarqués sur des satellites, mesurent la luminance puis déduisent une température équivalente de rayonnement (ou température de brillance), prise essentiellement sur l’oxygène, parfois sur le CO2.

C’est à partir de ces mesures brutes que l’on élabore (depuis les années 90) des indicateurs de température. L’université d’Alabama à Huntsville fournit l’indicateur UAH [1] , l’entreprise Remote Sensing Systems, en liaison avec la NASA, fournit l’indicateur RSS [2] . Les indicateurs concernent diverses couches de l’atmosphère. Nous nous intéressons à l’indicateur correspondant à la couche en contact avec la surface terrestre (Lower Troposphere LT de l’ordre de ≈ 7 km d’épaisseur). L’usage est de présenter l’indicateur sous forme « d’anomalie », c’est-à-dire l’écart par rapport à une température de référence.

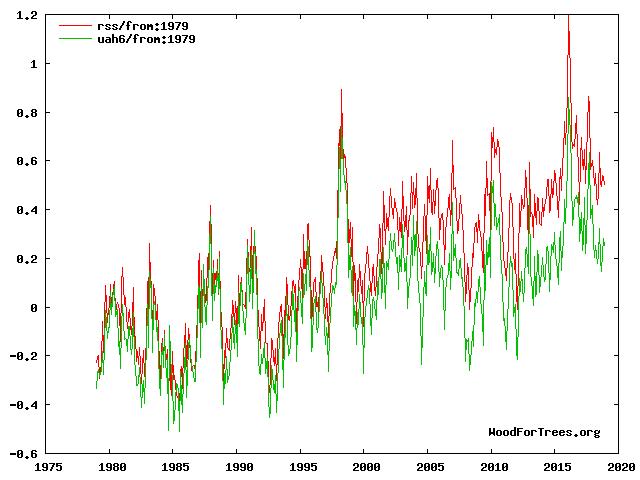
Figure 2a. Indicateurs UAH et RSS en valeurs mensuelles.

 

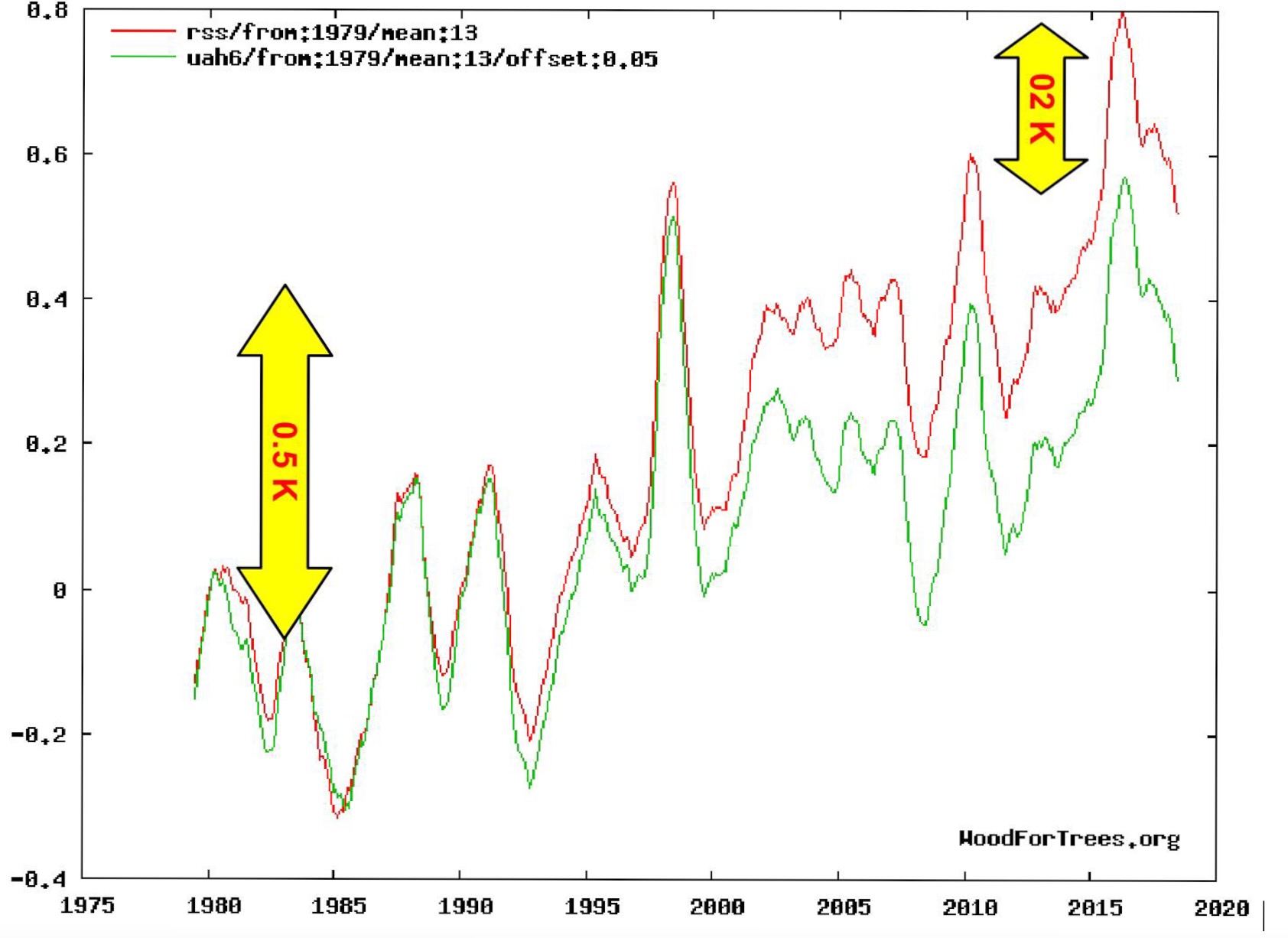
Figure 2b.  Indicateurs UAH et RSS en moyenne glissante sur 13 mois.
Il existe un désaccord ou un écart  ≈ 0.2 K entre RSS et UAH.

La distance Terre Soleil est variable dans l’année, ce qui a pour conséquence une variation ≈ 90 W/m² sur la puissance délivrée au sommet de l’atmosphère par le Soleil (en moyenne ≈1365 W/m²). Il est d’usage de prendre une moyenne glissante sur l’année pour les indicateurs (Fig. 2b). On constate que les indicateurs UAH ou RSS présentent une hausse de l’ordre de +0.5K en 40 ans soit une variation relative pour l’indicateur de 0.5/265 = 0.2% (« température moyenne » des premiers km d’atmosphère ≈ 265K contre ≈ 287K au sol).

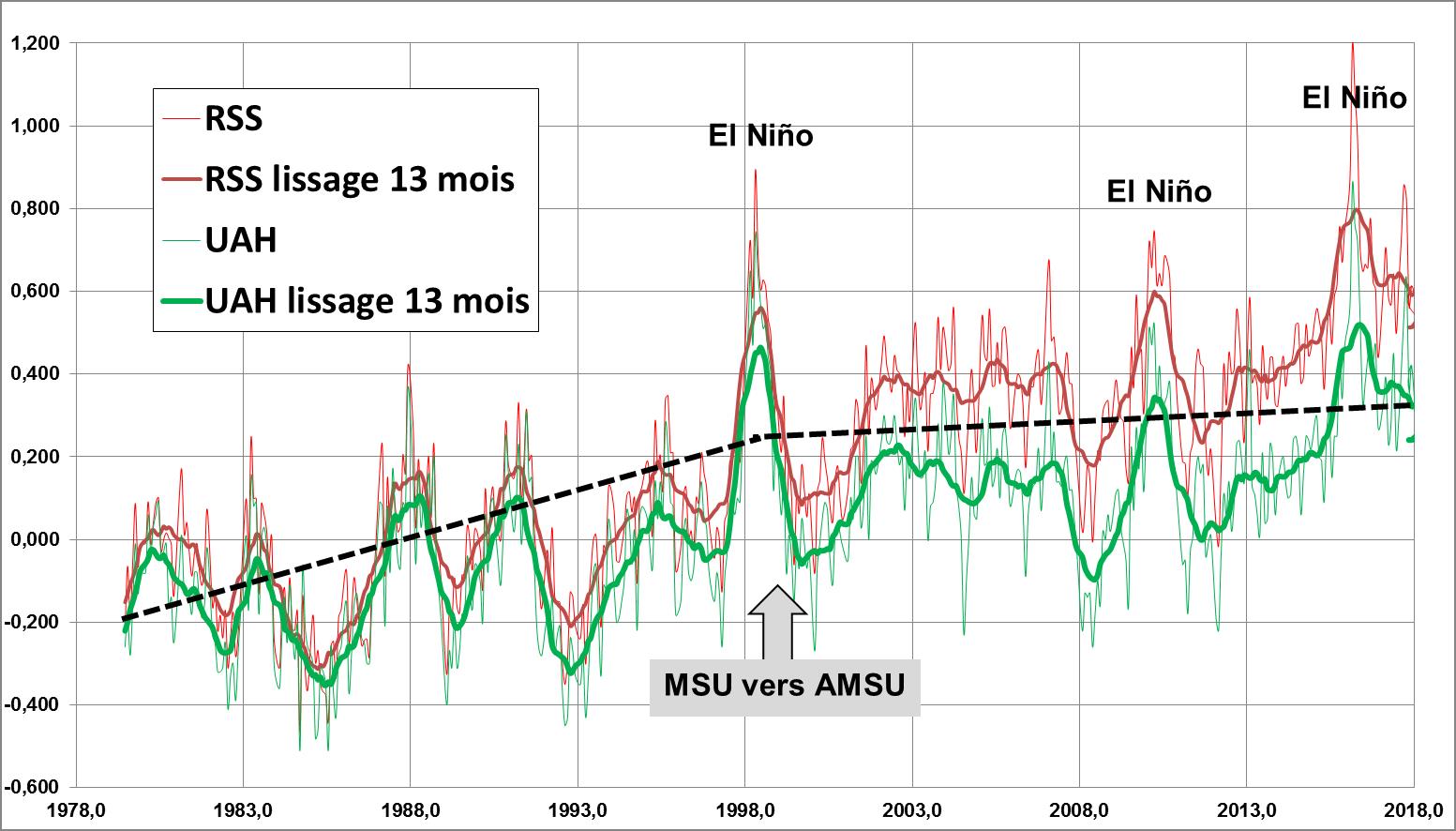 Figure 3a. [3] Les indicateurs RSS et UAH en valeurs mensuelles et en moyenne lissée sur 13 mois. On distingue 3 phénomènes naturels ENSO : El Nino 1998, 2010 et 2016. L’océan intertropical est donc responsable de variations transitoires supérieures à 0.5 K pour les indicateurs RSS/UAH. C’est aussi une conséquence du rapport des capacités thermiques océan/ atmosphère de la Fig.1.

Nous verrons, dans la partie 2 de l’article, qu’à la fin des années 90, on procède à un changement progressif d’instrumentation (ici slide 3 MSU vers AMSU). On remarque une double coïncidence → l’écart entre RSS et UAH augmente vers cette même date, et les pentes pour RSS ou UAH (trait pointillé Fig.3a ou bien ici) ) semblent légèrement plus prononcées avant 1999 que par la suite. 

Figure 3b.   [3]   (ou bien ici). On trace la différence entre la valeur mensuelle et la moyenne glissante sur 13 mois= variabilité mensuelle. Pour RSS c’est donc la différence entre les 2 courbes rouges de la Fig. 3a. Pour UAH c’est la différence entre les 2 courbes vertes de la Fig. 3a.

Il y a une bonne corrélation entre RSS/UAH pour la variabilité mensuelle. On trouve un écart type ≈ 0.1K [3] et une plage (max-min) ≈ 0.7 K.

Pour estimer la hausse moyenne des indicateurs, il est d’usage d’utiliser la tendance (pente moyenne) en K/décennie. Pour estimer la tendance, on va utiliser ici la différence entre les 5 premières années et les 5 dernières années afin d’effacer la variabilité mensuelle et l’influence ENSO (El Niño/La Niña).

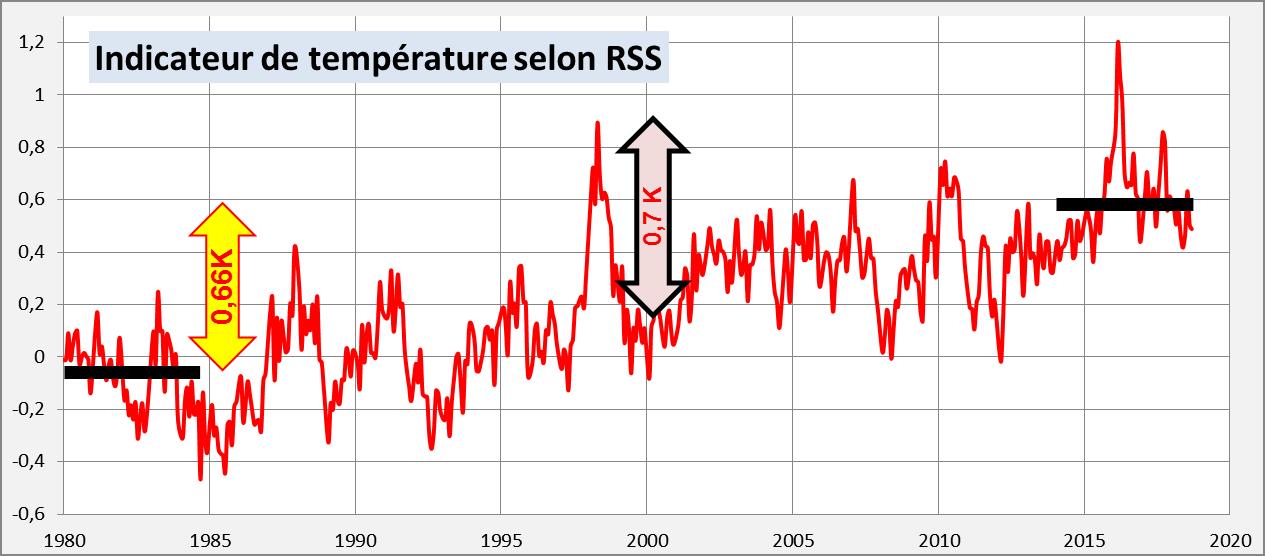
Figure 4a. [3] Les 2 traits noirs horizontaux sont les moyennes sur 5 ans = 60 mois. L’influence de El Niño 1998 est ≈ 0.7K. On a ≈ 35 ans entre le milieu des 2 traits noirs. Pour l’indicateur RSS la tendance ≈ 0.66/3.5 = +0.19 K/décennie.

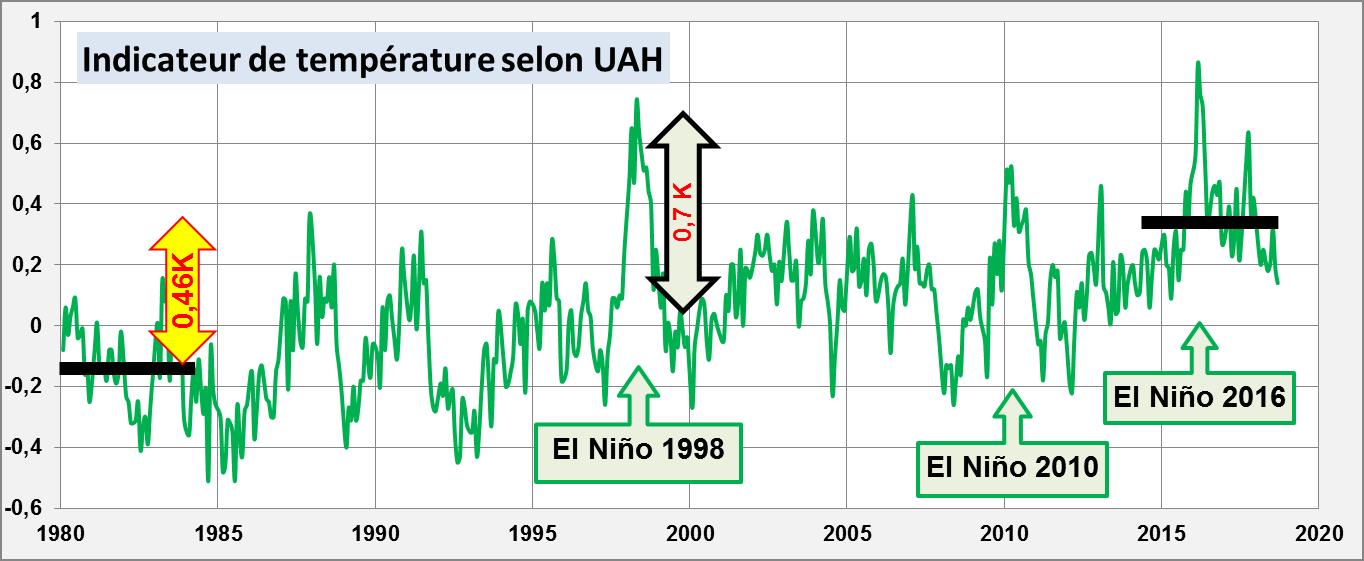
Figure 4b.  [3]  Pour l’indicateur UAH la tendance ≈ 0.46/3.5 = +0.13 K/décennie.

La tendance moyenne RSS/UAH ≈ 0.16 K/décennie. On peut remarquer que si cette tendance restait inchangée, la hausse serait de +1.3 K d’ici 2100.

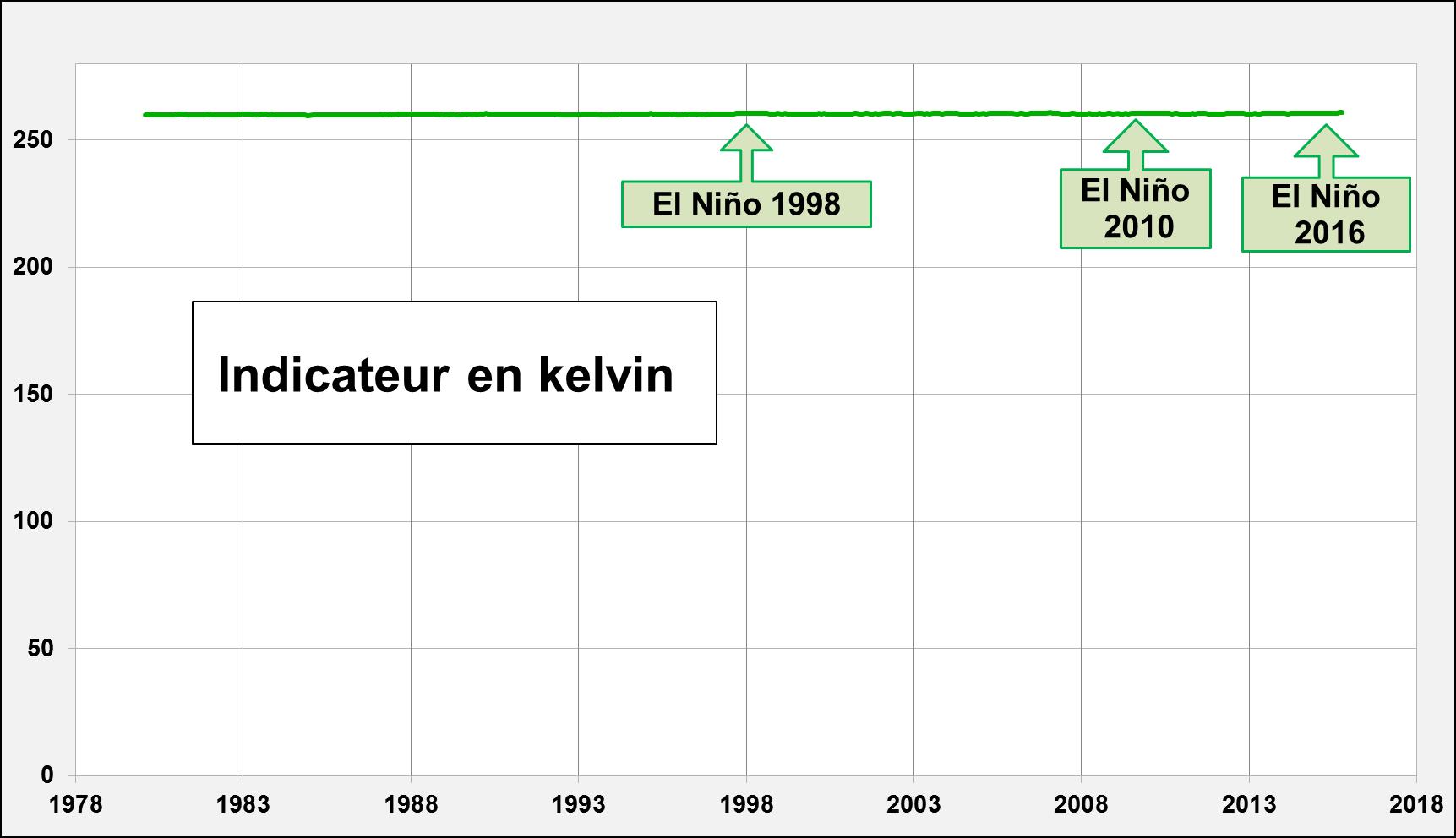
 Figure 4c. [3] On a utilisé pour les figures 2a, 2b, 3a, 4a et 4b une représentation sous forme « d’anomalie » en usage chez les climatologues, mais cela correspond à un fort zoom sur l’échelle verticale. Une représentation, rarement utilisée, est celle faisant apparaître l’indicateur de température sans zoom sur l’axe vertical→ Fig. 4c. Sous cette forme, la hausse +0.5K ou +0.2% ou +0.16 K/décennie est peu évidente, et on distingue à peine les phénomènes ENSO.

La modestie de la hausse relative ≈ + 0.2% mérite que l’on examine comment sont élaborés les indicateurs UAH ou RSS.

La marge d’erreur sur les indicateurs est-elle inférieure à 0.2%? Les indicateurs RSS et UAH, élaborés à partir des mêmes mesures de luminance, présentent une hausse en 40 ans (Fig.2b) qui diffère pourtant de 0.2K. Quelles sont donc les procédures de correction sur les données brutes ?

La deuxième partie (à suivre) examinera les mesures et les corrections qui permettent l’élaboration des indicateurs UAH et RSS.

Réferences

1   Indicateur  UAH     https://www.nsstc.uah.edu/data/msu/v6.0/tlt/uahncdc_lt_6.0.txt

2   Indicateur  RSS   http://images.remss.com/data/msu/graphics/TLT_v40/time_series/RSS_TS_channel_TLT_Global_Land_And_Sea_v04_0.txt

3    Feuille de calcul  « Températures satellites »